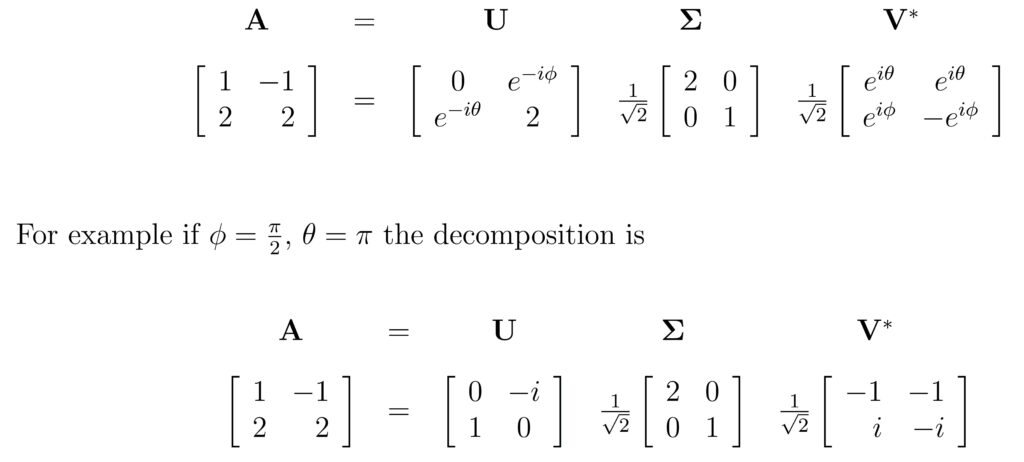Singular Value Decomposition (SVD) is one of the most fundamental matrix factorization techniques in linear algebra. It’s widely used in fields like data science, machine learning, and image compression. A Singular Value Decomposition calculator is an essential tool for anyone working with matrices, providing a quick way to break down complex matrix operations.
What is Singular Value Decomposition?
Singular Value Decomposition (SVD) is a method of decomposing a matrix into three smaller matrices:
- UU (left singular vectors),
- Σ\Sigma (a diagonal matrix containing singular values),
- VTV^T (right singular vectors).
For any real matrix AA, the SVD can be expressed as:
A=UΣVTA = U \Sigma V^T
Where:
- AA is the original matrix,
- UU and VTV^T are orthogonal matrices,
- Σ\Sigma is a diagonal matrix containing non-negative singular values of AA.
This decomposition helps reduce dimensionality, extract important features, or reconstruct matrices efficiently in a compressed format.
Applications of Singular Value Decomposition
The use cases of SVD span many domains, making a singular value decomposition calculator a crucial tool for anyone involved in data-heavy work. Here are some key applications:
- Data Compression: SVD helps in compressing large datasets by reducing their dimensionality. For example, in image compression, an image matrix can be decomposed using SVD to retain the most important features, discarding minor details, which reduces storage requirements without significant loss in quality.
- Noise Reduction: In signal processing and image processing, SVD can filter out noise by eliminating the smaller singular values (which often represent noise) while keeping the larger ones that represent the main signal or image features.
- Recommendation Systems: SVD is often used in machine learning models, particularly in recommendation systems (like Netflix’s recommendation algorithm), where it helps to analyze patterns in user preferences and item features to make accurate recommendations.
- Principal Component Analysis (PCA): PCA, a widely-used technique for dimensionality reduction, often utilizes SVD under the hood to project data into lower dimensions, making it easier to visualize and analyze large datasets.
- Natural Language Processing (NLP): In NLP, SVD is used to decompose large text-based matrices, such as those found in Latent Semantic Analysis (LSA). This allows for the discovery of hidden patterns and relationships in textual data.
How a Singular Value Decomposition Calculator Works
A singular value decomposition calculator simplifies the complex operations of breaking down matrices into their singular values and vectors. It provides a user-friendly interface where users can input their matrix data and get the decomposed components instantly. Here’s how it typically works:
- Input: The user inputs a matrix (which can be square or rectangular) into the calculator.
- Computation: The calculator computes the SVD by solving for the matrices UU, Σ\Sigma, and VTV^T. This involves:
- Finding the eigenvalues and eigenvectors of ATAA^T A (for VV) and AATA A^T (for UU).
- Diagonalizing the matrix to generate the singular values.
- Output: The calculator then displays the three components of the SVD: UU, Σ\Sigma, and VTV^T. Depending on the complexity of the calculator, it may also allow users to adjust tolerance levels to include or exclude small singular values.
Benefits of Using a Singular Value Decomposition Calculator
- Efficiency: A singular value decomposition calculator automates the process of SVD, which can be time-consuming if done manually, especially for large matrices. It saves users from writing code or performing complex calculations by hand.
- Accuracy: A calculator reduces human error that may occur when decomposing matrices manually. High-precision results ensure that downstream tasks, such as machine learning models or data compression algorithms, work as expected.
- Accessibility: For non-experts or those who are just learning about linear algebra, a calculator provides an easy entry point into understanding and working with SVD. You don’t need to know all the underlying theory to use the tool effectively.
- Versatility: Whether you’re working with small 2×2 matrices or large datasets with hundreds of dimensions, the calculator can handle it all. Many calculators also allow customization, such as truncating the number of singular values or vectors returned.
Features to Look for in a Singular Value Decomposition Calculator
When choosing a singular value decomposition calculator, look for the following features:
- Matrix Size Support: Ensure the calculator can handle the size of matrices you work with, especially if you deal with large datasets or high-dimensional matrices.
- Precision Control: Some calculators allow you to set the level of precision for singular values, which can be useful in applications like noise reduction or dimensionality reduction.
- Real-time Results: Many modern calculators offer real-time decomposition as you input matrices, which speeds up analysis and makes the process more intuitive.
- Integration with Other Tools: Look for calculators that integrate with data science or mathematical tools like Python, MATLAB, or Excel. This can streamline workflows if you need to switch between manual computation and automated tools.
Conclusion
A singular value decomposition calculator is an indispensable tool for students, researchers, and professionals working with matrices. Whether you are looking to reduce dimensionality, compress data, or clean noisy signals, SVD offers an efficient and effective solution. With its wide range of applications and the simplicity of using a calculator, you can quickly analyze and decompose matrices to achieve deeper insights into your data.
When selecting a singular value decomposition calculator, prioritize features like matrix size support, precision control, and ease of use to ensure it meets your needs. In the end, using such a calculator not only saves time but also enhances your ability to work with complex data more accurately and effectively.